Solutions¶

>>> from zero.solution import Solution

The Solution class provides a mechanism for storing, displaying and saving the output of an analysis; these are usually responses and noise spectral densities.

Retrieving functions¶

Solutions contain methods to retrieve functions contained within those solutions using a variety of filters. The methods filter_responses(), filter_noise() and filter_noise_sums() provide ways to match functions against their sources, sinks, groups and labels. These methods return a dict containing the matched functions in lists keyed by their group names (see Groups).

To retrieve an individual function directly, three convenience methods are available: get_response(), get_noise() and get_noise_sum(). These take as arguments the source, sink, group and/or label of the Response, NoiseDensity or MultiNoiseDensity to retrieve. The source and sink in get_response() and the sink in get_noise() and get_noise_sum() can be components or nodes or names, while the source in get_noise() can be a Noise or noise specifier such as V(op1). Sources cannot be searched against when using get_noise_sum(). You can use these convenience methods to retrieve functions when you know enough information about it to match it amongst the solution’s functions. If multiple functions are found as a result of the filters you provide, a ValueError is thrown.

The table below lists the available filters for the filter_ methods for each function type. With the exception of the multi-valued filters, i.e. sources, sinks, groups and labels, these parameters are also available when using the get_ methods.

Filter	Possible values	Responses	Noise	Noise sums
`source`	Source `Component`, `Node` or `Noise`	✓	✓	✗
`sources`	`List` of sources, or `all` for all sources	✓	✓	✗
`sink`	Sink `Component`, `Node`	✓	✓	✓
`sinks`	`List` of sinks, or `all` for all sinks	✓	✓	✓
`group`	Function group name (`str`)	✓	✓	✓
`groups`	`List` of group names, or `all` for all groups	✓	✓	✓
`label`	Function label (`str`)	✓	✓	✓
`labels`	`List` of labels, or `all` for all labels	✓	✓	✓

Specifying response sources and sinks¶

Response sources and sinks (and Noise sinks) specified in get_noise() are always components or nodes. You can specify these using either the corresponding Component or Node objects or by specifying their name as a string.

Assuming that a circuit is built in the following way…

>>> import numpy as np
>>> from zero import Circuit
>>> from zero.analysis import AcSignalAnalysis
>>> circuit = Circuit()
>>> circuit.add_opamp(name="op1", model="OP27", node1="gnd", node2="nin", node3="nout")
>>> circuit.add_resistor(name="r1", value="1k", node1="nin", node2="nout")
>>> signal_analysis = AcSignalAnalysis(circuit)
>>> solution = signal_analysis.calculate(frequencies=np.logspace(0, 4, 1001), input_type="voltage", node="nin")

…responses between the input node and various nodes and components can be retrieved in the following ways:

>>> nin = circuit["nin"] # get the input node object
>>> nout = circuit["nout"] # get the output node object
>>> print(solution.get_response(nin, nout)) # response between input and output nodes
nin to nout (V/V)
>>> print(solution.get_response("nin", "nout")) # alternative string specifier
nin to nout (V/V)
>>> print(solution.get_response("nin", "r1")) # response between input node and resistor current (note the units)
n1 to r1 (A/V)
>>> print(solution.get_response(label="nin to r1 (A/V)")) # label specifier
n1 to r1 (A/V)

Specifying noise sources and sinks¶

In order to retrieve a noise function from a solution, you must specify the noise source in get_noise(). Noise sources can either be specified using their noise object or by building a noise specifier string. Noise sinks are specified in the same way as response sinks (see above).

Specifying the noise source by its object involves first retrieving the component that produces the noise. Each component holds its noise sources in its properties. For example, op-amps have voltage noise at their output and current noise at their inverting and non-inverting inputs. Assuming the op-amp is referenced by op1, these can be retrieved using op1.voltage_noise, op1.inv_current_noise and op1.non_inv_current_noise, respectively.

An alternative approach is to use a noise specifier string. These are strings constructed in the form prefix(component-name[, node-name]), with the prefix representing the type of noise as shown in this table:

Noise type	Prefix	Example
Resistor (Johnson)	`R`	`R(r1)`
Op-amp voltage	`V`	`V(op1)`
Op-amp non-inverting current	`I`	`I(op1, np)`
Op-amp inverting current	`I`	`I(op1, nm)`

Assuming that a circuit is built in the following way…

>>> import numpy as np
>>> from zero import Circuit
>>> from zero.analysis import AcNoiseAnalysis
>>> circuit = Circuit()
>>> circuit.add_opamp(name="op1", model="OP27", node1="gnd", node2="nin", node3="nout")
>>> circuit.add_resistor(name="r1", value="1k", node1="nin", node2="nout")
>>> noise_analysis = AcNoiseAnalysis(circuit)
>>> solution = noise_analysis.calculate(frequencies=np.logspace(0, 4, 1001), input_type="voltage", node="nin", sink="nout")

…noise functions can be retrieved with e.g.:

>>> op1 = circuit["op1"] # get the op1 object
>>> print(solution.get_noise(op1.voltage_noise, "nout")) # voltage noise at op1
V(op1) to nout
>>> print(solution.get_noise("V(op1)", "nout")) # alternative string specifier
V(op1) to nout
>>> print(solution.get_noise(op1.inv_current_noise, "nout")) # current noise at op1's inverting input
I(op1, nin) to nout
>>> print(solution.get_noise("I(op1, nin)", "nout")) # alternative string specifier
I(op1, nin) to nout
>>> print(solution.get_noise(label="I(op1, nin) to nout")) # label specifier
I(op1, nin) to nout

Groups¶

Solutions support grouping as a means to keep different sets of functions separate, such as those from different analyses. In most cases, groups do not need to be considered when accessing, manipulating and plotting a solution’s functions, but they become important when solutions are combined.

By default, functions are added to a solution’s default group. Functions can be added to another group by passing the group parameter to one of add_response(), add_noise() or add_noise_sum(). Groups can be renamed with rename_group() and merged with merge_group(). The functions in the default group can be moved to a new group with move_default_group_functions().

Plotting with groups¶

When a solution containing multiple groups is plotted, the functions in each group have different formatting applied. The colours of functions within each group follow roughly the same progression as the first group, but with gradually lighter shades and different line styles.

To plot functions from different groups without different shades or line styles, you should combine them into the same group (see above).

Combining solutions¶

Solutions from different analyses can be combined and plotted together. The method combine() takes as an argument another solution or multiple solutions, and returns a new solution containing the combined functions.

Warning

In order to be combined, the solutions must have identical frequency vectors.

Solutions can be combined in two ways as determined by combine()’s merge_groups flag. When merge_groups is False (the default), the groups in each source solution are copied into the resulting solution. The default group in each source solution is copied into a group with the name of the corresponding source solution, and other groups have the corresponding source solution’s name appended in brackets. This form of combination supports the sol_a + sol_b syntax. When merge_groups is True, the groups in each source solution are merged in the resulting solution. This requires that the source solutions contain no identical functions in cases where the group names are the same (including the default group).

The resulting solution’s group names can be changed using rename_group().

Hint

Solutions containing different types of function can be combined, such as solutions with the results of signal analyses and solutions with the results of noise analyses. In order to plot all of the combined solution’s functions in such a case, you must call both plot_responses() and plot_noise().

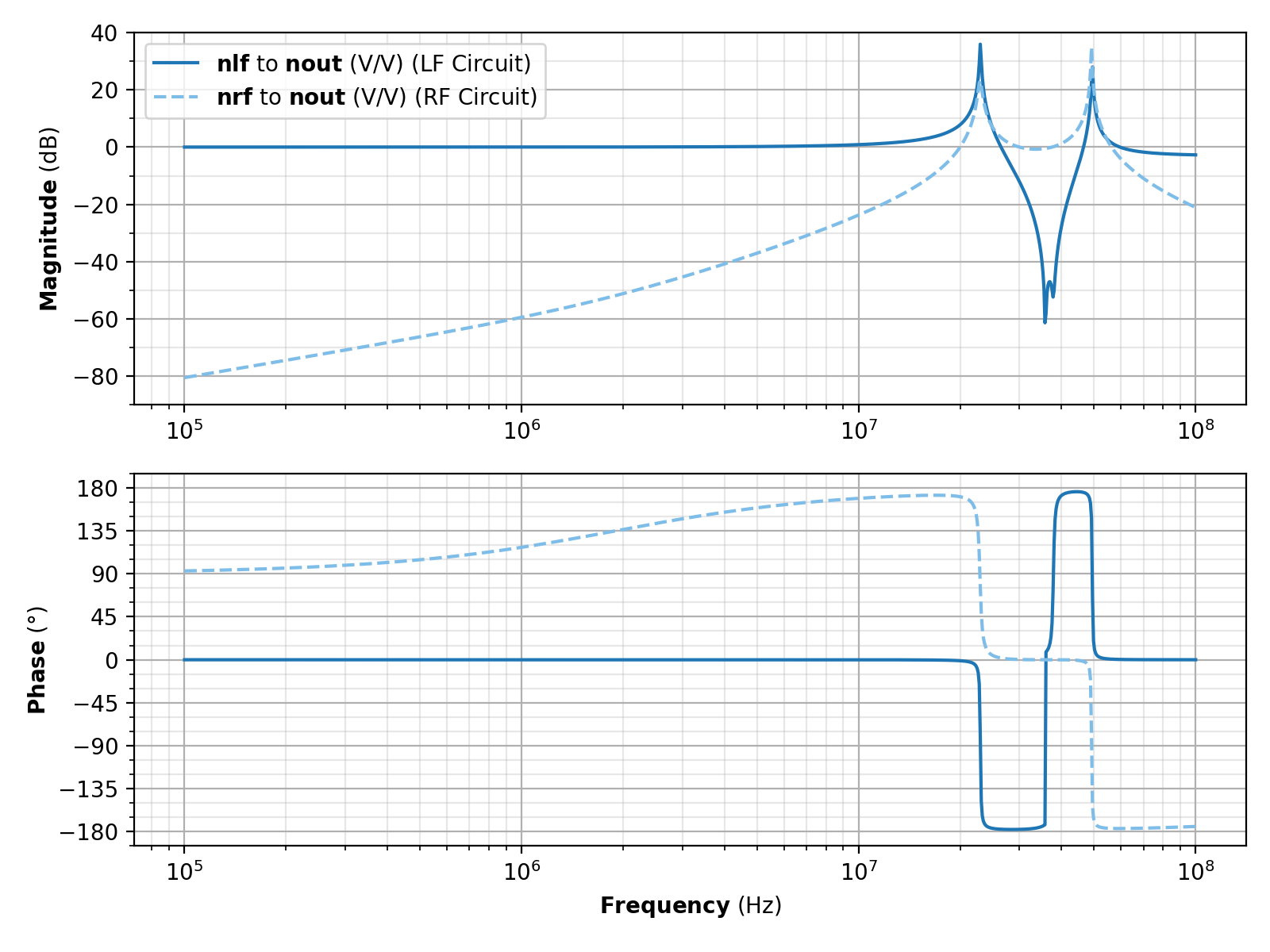
Here is an example of solution combination using a LISO model of an RF summing box with two inputs and one output:

from zero.liso import LisoInputParser

# Create parser.
parser = LisoInputParser()

base_circuit = """
l l2 420n nlf nout
c c4 47p nlf nout
c c1 1n nrf gnd
r r1 1k nrf gnd
l l1 600n nrf n_l1_c2
c c2 330p n_l1_c2 n_c2_c3
c c3 33p n_c2_c3 nout
c load 20p nout gnd

freq log 100k 100M 1000
uoutput nout
"""

# Parse the base circuit.
parser.parse(base_circuit)
# Set the circuit input to the low frequency port.
parser.parse("uinput nlf 50")
# Ground the unused input.
parser.parse("r nrfsrc 5 nrf gnd")
# Calculate the solution.
solutionlf = parser.solution()
solutionlf.name = "LF Circuit"

# Reset the parser's state.
parser.reset()

# Parse the base circuit.
parser.parse(base_circuit)
# Set the input to the radio frequency port.
parser.parse("uinput nrf 50")
# Ground the unused input.
parser.parse("r nlfsrc 5 nlf gnd")
# Calculate the solution.
solutionrf = parser.solution()
solutionrf.name = "RF Circuit"

# Combine the solutions. By default, this keeps the functions from each source solution in
# different groups in the resulting solution. This makes the plot show the functions with
# different styles and shows the source solution's name as a suffix on each legend label.
solution = solutionlf.combine(solutionrf)

# Plot.
solution.plot()
solution.show()

(Source code, png, pdf)

Hint

The above example makes a call to plot(). This relies on default functions having been set, in this case by the LISO compatibility module, which is normally not the case when a circuit is constructed and simulated natively. In such cases, calls to plot_responses() and plot_noise() with filter parameters are usually required.

Default functions¶

Default functions are functions that are plotted when a call is made to plot_responses() or plot_noise() without any filters. Functions are not normally marked as default when an analysis builds a solution.

A function can be made default by setting the default flag to True when calling add_response(), add_noise() or add_noise_sum().

Note

When a LISO script is simulated by Zero, the functions plotted by the LISO script are marked as defaults. This behaviour assists when comparing a LISO solution to that of Zero, since LISO does not output every possible response or noise whereas Zero does. In this case, only the functions that are requested in the LISO script are set as defaults in the Zero solution, so that only the relevant functions are compared.